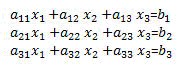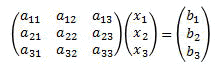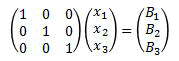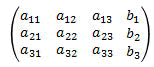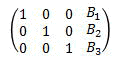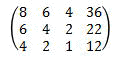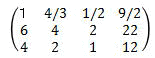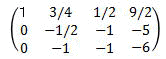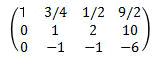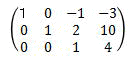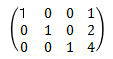連立1次方程式の解（ガウスの消去法）

ガウス（Gauss）の消去法は連立一次方程式を解くのに用いられます。
下記のような連立一次方程式(ここでは3元一次を例にとる)を

この連立一次方程式を行列で表すと

このようになり、 この行列の対角成分を全て１、 それ以外の成分を全て０になるようにすると、

となりの解が出ます。  このの行列式を抽象化すると

このようになり 行の入替、足し算、引き算、掛け算、割り算をしても 行列式は変らないため

この行列に変形して解を得る。

対角成分の数値をピポットと言いい
ピボットを大きく選びながら（行の入替をする）ガウスの消去法を適用すれば
誤差を抑え，精度の良い解を得ることができる。

順	行列の内容	処理例
1		１行目１列目（ピポット）が１になる様に １行目を８で割る
2		２行目、３行目の１列目が消える様に ２行目－１行目×６、３行目－１行目×４を計算する
3		２行目２列目（ピポット）が１になる様に ２行目を-1/２で割る
4		１行目、３行目の２列目が消える様に １行目－２行目×（３／４）、３行目＋２行目を計算する
5		１行目、３行目の３列目が消える様に １行目＋２行目、２行目－３行目×２を計算する
6		３行目、３列目（ピポット）が１であるので、 解は１、２、４です。